The Real Meaning of To Infinity and Beyond!

Yes, I went there. I finally acknowledged the elephant in the room, and I am writing now about the most used and abused quote about infinity.

To... boundlessness and... above?

I'm talking of course about the infamous catchphrase of Buzz Lightyear in Toy Story or, as Imdb puts it:

[repeated line] 
Buzz: To infinity, and beyond! 

What is the meaning of "To infinity and beyond?" 

It seems a throwaway line, but hidden there is a deep philosophical meaning. It pops up here and there in pop culture and even in random discussions with friends. In 2001: A Space Odissey just before the psychedelic "Star Gate" sequence a title card appear, "Jupiter and Beyond the Infinite" (an inspiration for Buzz?). In the hit Single Ladies (Put a Ring on It), Beyoncé sings "... and delivers me to a destiny, to infinity and beyond.", There are then the album Beyond the Infinite, by trance group Juno Reactor, or the Greek film Eternity and a Day, by director Theo Angelopoulos. In 2008 this sentence helped father and son to survive a shipwreck. And let's not forget infinity plus one! And the lovey-dovey couples smooching "I love you infinity times and more". There are probably infinite other examples (and more!). 

It sounds paradoxical: how can you go beyond the infinity? It's not possible to reach the end of infinity (because it is infinite), so how can one overtake it? One needs to change completely point of view: from potential infinity to actual infinity.

Let me go back to the example of Achilles and the tortoise, just like this blog started. You have the tortoise and Achilles, say, 10 meters apart, Achilles in the back. They run. Achilles is much faster than the tortoise, so when Achilles reached the point where the tortoise was, the tortoise just made one meter. Achilles run that meter, and the tortoise is 10 cm ahead. And so on, and so on. Will Achilles ever reach the tortoise?

If you have the mentality above, it will not: you have this infinite succession of states: 10 m distance, 1 m distance, 10 cm distance, ... and you cannot reach the end of it, because it is infinite! This is the so-called potential infinite, potential because you never realize it in full, you just see parts of it.

But we know that Achilles reaches the tortoise, right? We're not that stupid. So what? Well, this is where Cantor shines! He managed to treat in a formal way the actual infinite. You pick all the infinity, you put it in a sack, and you treat it as a whole, completed object. So you can imagine what happens after it, in this case Achilles overtake the tortoise, turns and makes very funny faces. "Brlbrblrblrl".

Think of the potential infinity as an infinity you are walking inside. Like, just go out now and try to reach the horizon, it will always go on and on and you will never reach it. But the actual infinity is like seeing everything from above, so instead of walking pick a drone and go up, up, up, and you can embrace everything with a single view. (Of course, the metaphor works only if our Earth is flat and infinite, sorry, so I guess that makes no sense).

Another Zeno's Paradox: the dichotomy paradox. You have to go to a bus station that is 1 km far. To go there, you have to go half kilometer far. And then a quarter kilometer more. And then an eighth more. How can you reach the bus station? In mathematics, the distance you make is written like this:

According to a potentialist, this makes a potential 1, that is, is closer and closer to 1 without ever reaching it. According to an actualist, this is 1. What is the difference, you say? Look at this:

How much is this? According to an actualist, it is 2. According to a potentialist, it is BLAARGH GET THAT AWAY FROM MY FACE! SATAN!

Artist's rendition

The potentialists say that this is just a trick, that our limited minds just cannot comprehend actual infinities, and yet, mathematics goes just smoother with them, and the paradoxes are solved. Thanks, Cantor!

You know what? Let me see what the Internet thinks that "To infinity and beyond" means...

Oh, boy.

Fun fact: there are many, many mathematicians, even big experts, even Fields medals, that just have no clue about this. They work in mathematics like they were in the 19th century, willfully ignoring that all their work is founded on this.

This is the first results in Google (hopefully the second after I post this).

Definition in Mathematical Circles:
What exactly does Buzz Lightyear mean when he says, "To Infinity and beyond!"? A few professionals at Harvard investigated the origin of this quote and traced it back to limits. According to Dr. Sanjay Gupta, "Buzz Lightyear is a metaphor of a function which approaches a certain number, but never actually reaches it." However, experts at MIT believe that Buzz Lightyear is referring to vertical asymptotes. Dr. Benjamin Hernandez says, "It is possible to cross horizontal asymptotes, but verticals are impossible. Buzz Lightyear is showing everyone that he can do the impossible and cross horizontal and vertical asymptotes."

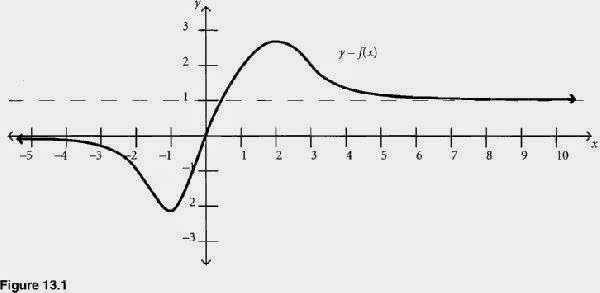
Now, I don't know who are these guys. Most probably they are misquoted, maybe they don't exists, so I am not really against them. But what is written there, trying to sound professional as heck (Harvard! MIT! Bum!) is far-reaching or just nonsense. The first sentence, by Dt Sanjay Gupta, is a typical expression of potential infinity (it approaches a certain number but never actually reaches it) and does not explain anything. Where is the beyond? The second sentence makes more sense: here is a horizontal asymptotes:

The asymptote is that dashed line. See? The function crosses it. Here is a vertical asymptote:

The function doesn't cross the line. And Buzz can! Well, OK, but... isn't this a little bit too technical? Also, isn't it a bit underwhelming that "Infinity and beyond" means a little bump in a line, just like your body when you eat too much Marshmallow Fluff?

INFINITY!

So, forget about what you read online. The meaning of "To infinity and beyond", even mathematically, is: we all think that we are trapped in our human limits, without escape, but in the end it is just an illusion. Buzz (and Cantor) is showing us the way to recognize the illusion, change the perspective, finally break free and go! leaving all our chains behind, going were it was previously unthinkable, unimaginable.

You hear that, potentialists?

PS. I am actually going to Harvard next week. If I meet Dr. Sanjay Gupta, I'll let you know.

Statistics says that probably this is the first page of the blog you are reading. Then, may I suggest to read the manifesto, to understand what is this about? Or just skip to the meaty parts, like the posts on "The Fault in Our Stars", or "The Big Bang Theory", or a cute AT&T advertisement.

One Reinhardt and counting...

The original post has been changed: the attribution of the game has been clarified.

Can you hear it? Do you hear that sound? It's something like streeeeeeeeaaaaaaatch. It's me stretching the theme of the blog to accomodate this topic.

You know 2048? Of course, everybody knows it. It's a very addicting game by Gabriele Cirulli, and the Wall Street Journal called it "almost Candy Crush for math geeks".

 Addiction has a face.

I cannot describe it.  Just play it. Or don't! You have to read this blog, don't get distracted.

The game is open source, so anybody can make a personal version. But then, don't you feel that the numbers here are a bit... small? 2048 is so tiny, is there a way to go really big?

If you dare to adventure the deep, deep academia web you'll find a specific version... with large cardinals! Now also you can climb up the large cardinals hierarchy! The name of the game is Reinhardt. The original idea was by Yizheng, and then it was picked up by Chris La Sueur, that changed the large cardinals and published it.

Now, Chris is so kind to suggest you not to play to the big version, but I am evil and I push you to try that instead of Reinhardt. It is called 1=0, and it is cleaner and more strategical.

I thought about giving you the list of the cardinals involved, but why ruining the fun? Part of the delight is in the exploration!

But why it is called Reinhardt? This is the skeleton in the closet of all set theorists.

The reaction of set theorists when asked about Reinhardt and large cardinals

Once upon time (1969, to be precise), William Reinhardt was studying some large cardinal, and had an idea: to build the largest cardinal ever, the king of large cardinals, the most powerful! We now call it Reinhardt cardinal.

But just after months, Kenneth Kunen proved that it was too big and powerful. In fact it just couldn't exist! Set theorists wanted the absolute power, but they overshot and reached a contradiction, and now the tale of the non-existing Reinhardt cardinal is taught to all students, as a sombre reminder that in trying to achieve too much, one risks to destroy everything. Anyway, Reinhardt cardinal is the largest cardinal, even if it does not exists, and the aim of the game is to reach it.

And why the big one is called 1=0? This is more difficult to say, probably I will write it in another post. (Edit: here it is!)

Now you can go playing! Have a nice waste of time!

Many large cardinals that appear in the game already appeared here. Interested in just one large cardinal? Make it this one, says Sheldon.